《心理统计学》知识点：第三章 集中量数

天任考研小编为大家整理了“《心理统计学》知识点：第三章  集中量数”相关内容，为报考心理学专业的考生们提供指导。更多有关心理学知识点可关注考研备考栏目。

第三章  集中量数

一、算数平均数

（一）概述

1.含义

数据总和除以数据个数，简称为平均数或均数，用M表示。平均数是一个平衡点，是一组数据的重心。

总体参数：μ，样本统计量：

 ̅

2.特点

（1）在一组数据中每个变量与平均数之差（称为离均差）的总和等于零。另外，离均差的平方和最小，即每个数据与平均数之差的平方和都小于每个数据与任一常数之差的平方和，也即平均数的“最小平方”原理。

（2）在一组数据中，每一个数都加上一个常数C，所得的平均数为原来的平均数加常数C。

（3）在一组数据中，每一个数都乘以一个常数C，所得的平均数为原来的平均数乘以常数C。

3.评价

（1）优点：反应灵敏、计算严密、计算简单、简明易解，适合进一步用代数方法演算，较少受抽样变动的影响。

（2）缺点：易受极端数据的影响，不能在出现模糊数据时计算。

4.应用

算数平均数是应用最普遍的一种集中量数，它在大多数情况下是真值最好的估计值。在应用时要注意以下原则：同质性原则、平均数与个体数值相结合的原则、平均数与方差及标准差相结合的原则。

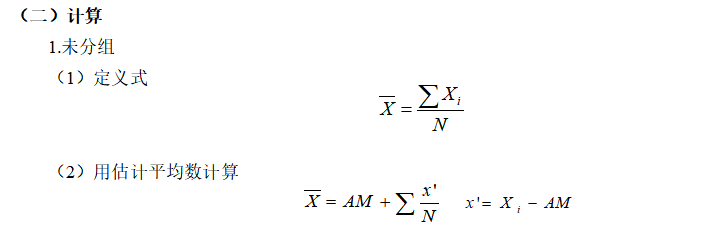
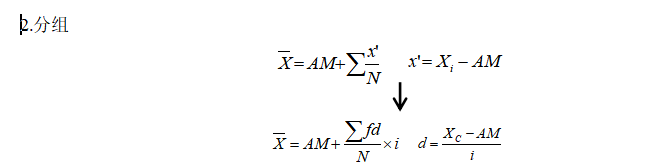
（三）其他

加权平均数适合解决用各个平均数求整体总平均数之类的问题。

倒数平均数适合解决求平均速率一类的问题。

几何平均数适合解决求增长比率的平均数一类问题。

二、中数

（一）概述

1.含义

中数是按顺序排列在一起的一组数据中居于中间位置的数，用M_d表示。在这组数据中，有一半数据比它大，一半数据比它小，等价于百分位数是50的那个数。

2.评价

（1）优点：计算简单、容易理解、不受极端值影响。

（2）缺点：代表性差、不够灵敏、稳定性低、需要排序、不能做进一步的代数运算。

3.应用

①存在极端数值和偏态分布；

②存在未确定数值；

③尾端开放式分布；

④存在顺序型数据。

三、众数

（一）概述

1.含义

众数是次数分布中出现次数最多的那个数的数值，用M_O表示。众数可能不止一个。

2.评价

（1）优点：容易理解、能避免极端值干扰。

（2）缺点：代表性差、不够灵敏、不稳定、不准确、不能做进一步的代数运算。

3.应用

①存在极端数值或双峰分布；

②离散变量；

③当需要快速地粗略地求出一组数据的代表值时；

④存在称名型数据。

（二）计算

1.直接观察

2.公式法：M_O=3M_d-2M

四、平均数、中数、众数三者的关系

1.正态分布：平均数、中数、众数相等，三值重合。

2.偏态分布：平均数最靠近尾端；中数位于平均数与众数之间。

  正偏态分布： M_O<M_d<M ；负偏态分布：M<M_d<M_O

以上是天任考研小编为大家带来的“《心理统计学》知识点：第三章  集中量数”，希望考生们都能备考顺利，考上自己心仪的院校。想了解更多心理学专业备考相关内容请关注考研备考栏目。